In the Broomball Caucus conference, we’ve been debating whether to separate teams into softcore and hardcore leagues. Jack Delahanty wrote against splitting the league, because it would (he asserts) increase forfeits:

There's one problem, though - teams that are comprised of [softcore players] do have fun, and they deserve to be able to have fun. The problem is that these are also the teams that tend to forfeit games. The same players that enjoy sliding around on the ice and hanging out with their floor also TEND to be (and I'm not accusing anybody here, just observing a trend) the players that won't show up when it's cold, when they've got homework to do, or when they have some other thing going on. I'm not saying that players who enjoy broomball for the sake of sliding around don't deserve respect and consideration - they absolutely do. But I am saying that we had a huge problem with forfeits this year that has extended into the playoffs, and we should definitely not gear the league or even one division in the league to teams that are apt to forfeit. Forfeits, more than 12-0 losses, are the real evil that needs to be addressed.

I totally agree that forfeits are a big problem: you make space in your schedule, put on all your pads and cold-weather gear, get onto the ice, wait 15 minutes, and then don’t get to play! On the other hand, I got to thinking about this, and realized it’s not actually true that forfeits would get worse with multiple leagues. In fact, splitting games up into leagues which are correlated with a propensity for forfeiting actually reduces the chances any given game in the league will be forfeit.

Assume there are two types of teams, half with probability to forfeit a, and half with b, where a < b.

Case 1: Place all a teams in hardcore, and b teams in softcore. The probability of a forfeit in any hardcore game is twice the probability for one team to forfeit (a), and one team to show up (1-a), so we have p(forfeit) = 2a(1-a), and likewise for softcore. The average probability of any game being forfeited across the league is a(1-a) + b(1-b).

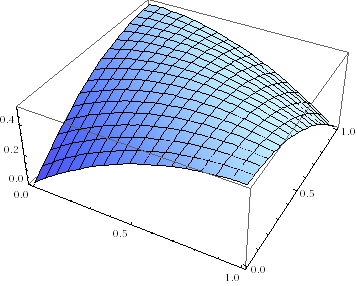
Case 2: Place all teams in one league. The probability any given game will be forfeit is just like for one league above, but with the average of the two probabilities: (a+b)(1-(a+b)/2).

Note that I’m talking about forfeits where one team fields and the other doesn’t: obviously, if neither team shows up, nobody really lost anything.

Okay, so now plot the average probability that a game will be forfeit for the two cases. In the split case, you’ll see it falls off sharply towards all corners: if absolutely NO softcore people show up, and all hardcore people do, there are no (problematic) forfeits.

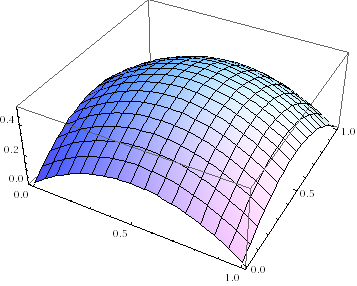
If you keep everyone in the same league, a few beginning teams forfeiting means that even the advanced teams have some probability of not being able to play, and the overall probability of forfeits rises.

Now look at the two cases superimposed. The split league scenario is at worst equal to the single league, and better in all other cases.

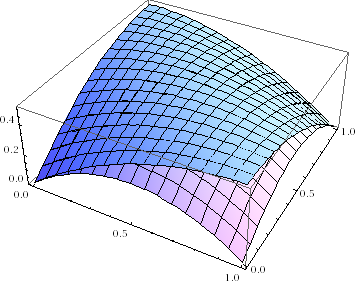
Long story short, all else being equal, leagues split by forfeit ratio are optimal for reducing the overall number of forfeit games. This assumes that the probabilities of forfeits aren’t affected by the establishment of leagues. My personal suspicion is that separate leagues increase the likelihood of play, because people aren’t scared of playing totally impossible games, but that’s up for debate. :-)